Detailed explanation of Linear Regression
1.1 Introduction
In a data set we can characterize features or variables as either quantitative or qualitative (also known as categorical). Quantitative variables are nothing but numerical values like a person’s weight or temperature of a city and qualitative variables are values in one of ’n’ different classes, or categories like gender (male or female), different blog categories(technical, cooking, fashion etc.,). We tend to refer to problems with a quantitative response as regression problems. The response variable here is referred to as target or dependent variable and the other independent variables are predictors.
Linear regression is used for finding linear relationship between target and one or more predictors. There are two types of linear regression- Simple and Multiple. In Simple linear regression we find the relationship between a dependent Y and independent variable X, the mathematical equation that approximates linear relationship between X and Y is

β0 and β1 are two unknown constants that represent the intercept and slope terms in the linear model. Together, β0 and β1 are known as the model coefficients or parameters. Once we have used our training data to produce estimates ˆβ0 and ˆβ1 for the model coefficients,

where ˆy indicates a prediction of Y on the basis of X = x.

represents the i th residual (error) which is the difference between the actual i th response value and the i th response value that is predicted by our linear model. We define the residual sum of squares (RSS) as

which is equivalent to

In regression, there is always a notion of a best-fit line — the line which fits the given data in the best way. RSS here is called loss function or cost function and minimizing it would result in good fit or accuracy. This approach is called least squares method. Least squares method chooses ˆβ0 and ˆβ1 to minimize the RSS using some calculus. Then a new set of coefficients are generated and we need some metrics to validate the accuracy of these estimated coefficients.
Here comes a set of metrics that help to perform the validating task easy:
1.2 Validation of Estimated Coefficients
- Standard Errors associated with ˆβ0 and ˆβ1,

where sigma is standard deviation,

In general Var(Error) is not known and it is approximated from the data as Residual Standard Error

2. We now compute t-static that measures the number of standard deviations ˆβ1 is away from 0

3. The probability of observing any value equal to |t| or larger, assuming β1 =0(which implies there is no relation ship between X and Y) is called p-value. A small p-value indicates it is an unlikely event that β1 = 0 and that Y is dependent on X or a relation exists between X and Y. Similarly a high p-values indicates no relation and X is insignificant in predicting Y.
1.3 Assessing Model Using Metrics
These metrics are useful in estimating the accuracy of coefficients. So now we can model with updated coefficients or features and evaluate the accuracy of this model. The extent of fit of linear regression is generally assessed with two Metrics
1. RSE can be defined in different terminologies
— The RSE is an estimate of the standard deviation of error
— The average value that the dependent variable deviated from the true-regression line or
— Lack of fit of the model
2. R-Squared statistic
— As RSE is measured in the units of Y we are never sure of what value is a good RSE. But R-squared is measured as proportion of variability in Y that can be explained using X and always will be range of 0 to 1 unlike RSE.
— Formula of R-squared is


— Total Sum of Squares measures the total variance or the inherent variance present in the response variable Y before the regression was performed.
— A value near 0 implies the model is unable to explain variance and a value close to 1 says model is able to capture the variability. A good performing model would have the R2 score close to 1
1.4 Assumptions in Linear Regression
The regression has five key assumptions:
- Linear relationship: linear regression needs the relationship between the independent and dependent variables to be linear. It is also important to check for outliers since linear regression is sensitive to outlier effects. The linearity assumption can best be tested with scatter plots.
2. Normal Distribution of error terms: If the error terms are non- normally distributed, confidence intervals may become too wide or narrow i.e., unstable. This does not help in estimation of coefficients based on cost function minimization.
3. No auto-correlation: The presence of correlation in error terms drastically reduces model’s accuracy. This usually occurs in time series models where the next instant is dependent on previous instant. The estimated standard errors tend to underestimate the true standard error as the intervals become narrower. This further results in reducing p-value which results incorrect conclusion of an insignificant variable.
4. Heteroscedasticity: The presence of non-constant variance in the error terms results in heteroscedasticity. Generally, non-constant variance arises in presence of outliers or extreme leverage values causing the confidence interval for out of sample prediction to be unrealistically wide or narrow.
5. No or little multi collinearity: Two variables are collinear if both of them have a mutual dependency. Due to this,it becomes a tough task to figure out the true relationship of a predictors with response variable or find out which variable is actually contributing to predict the response variable.
— This causes the standard errors to increase. With large standard errors, the confidence interval becomes wider leading to less precise estimates of coefficients.
1.5 Feature Engineering
As we talked about collinearity ,there are a few points to be marked. Collinearity of variables is found by plotting a co relation matrix and we eliminate one of the correlated variables that do not add any value to the model. After eliminating the them reconfigure the correlation matrix and continue eliminating till all the variables are independent of each other.
Instead of inspecting the correlation matrix, a better way to assess multi- collinearity is to compute the variance inflation factor (VIF). The smallest possible value for VIF is 1, which indicates the complete absence of collinearity. VIF value that exceeds 5 or 10 indicates a problematic amount of collinearity.
This is one of the feature engineering steps. Now train the model and check the metrics that define the accuracy and based on p-values we can eliminate the variables to reach an optimal score.This is performed directly in python packages.
1.6 Stochastic gradient Descent (SGD)
We can measure the accuracy or how good the model is fit with the measure Mean Squared Error(MSE) which calculates the mean of squared terms of difference between actual and predicted values

To optimize the model we have to reduce the MSE, we define loss function (L) which is equal to MSE and by a set of iterative steps we subtract the negative derivate of loss and update it at each step so that MSE or L is reduced. To calculate the negative derivative we use Stochastic Gradient method which helps in finding the global minimum of a function(here Loss function).
If we can imagine the function as shown in the figure,

the red dot is global minima and if the function is able to reach the estimated coefficients there, then it will be minimized resulting in better accuracy. Shifting the model to go in the steepest downhill direction would be the equivalent of subtracting the negative derivative of the loss, times some constant. Thus, we can formalize gradient descent for this problem as an update rule

it keeps on updating based on the gradient. α is the learning rate, and it affects how quickly m changes(m here refers to β in the convention used above)
2. Python Tutorial on Linear Regression
Let’s get into the practice session in python using beer consumption dataset that has temperatures of a particular day, rainfall measure,weekend or not and final response variable consumption of beer in liters. All the dependencies are resided in the top lines
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.stats.outliers_influence import variance_inflation_factor
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_scorebeer_data=pd.read_csv(“beer_consumption_data.csv”) #read csv data #into a dataframe using pd.read_csvbeer_data.head(10) #head() prints top 5 rows in the data set

As we see that the column names are in different language we can rename them by using the following command
beer_data.columns=[“Date”,”Temperature_Median”,”Temperature_Min”,”Temperature_Max”,”Rainfall”,”Weekend”,”Consumption_litres”]Also another observation is that temperature values and rainfall have comma instead of a dot to denote the number and they should also be converted to float or double as shown below
beer_data[‘Temperature_Median’] = beer_data[‘Temperature_Median’].str.replace(‘,’, ‘.’).astype(‘float’)
beer_data[‘Temperature_Min’] = beer_data[‘Temperature_Min’].str.replace(‘,’, ‘.’).astype(‘float’)
beer_data[‘Temperature_Max’] = beer_data[‘Temperature_Max’].str.replace(‘,’, ‘.’).astype(‘float’)
beer_data[‘Rainfall’] = beer_data[‘Rainfall’].str.replace(‘,’, ‘.’).astype(‘float’)beer_data.info() #info() outputs total number of rows,number of #columns and null values present in each of them.

#drop Blank rows read from the input CSV and describe shows all #statistics
beer_data = beer_data.dropna()
beer_data.describe()
Primary analysis on data is done and now we have to separate the predictor and response variables(here it is consumption_litres).As date is of no use and consumption_litres is a response variable, we separate them from other variables to perform the analysis and training. Then save them in different data frames.
X = beer_data.drop(columns=[‘Date’, ‘Consumption_litres’])
Y = beer_data[‘Consumption_litres’]Now that X and Y are obtained, we perform some tests like collinearity as discussed in section 1.5. We can do it by checking correlation matrix and VIF.
- Analyse with correlation matrix plot or heat map that gives the score of collinearity in range of 0 to 1.
- 1 being highly collinear and 0 being no mutual dependency.
- We can plot this using heatmap in seaborn library in python which we imported with name sns in the first step
- The argument to this heatmap will be X.corr() which gives the pairwise correlation of all columns of X in the dataframe
plt.figure(figsize=(7,7))
sns.heatmap(X.corr())
plt.title(“Correlation Heatmap”)
plt.show()
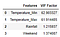
In the heat map here we can see that the Temperature_Median, Temperature_Min, Temperature_Max are highly collinear as their score is close to 1. Let us eliminate the unwanted features using VIF in next steps
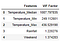
vif = pd.DataFrame() #Let us show th VIF scores in a data frame
vif[‘Features’] = X.columns
vif[‘VIF Factor’] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])] #variance_inflation_factor calculates the scores #for each Feature
vif
As we can see here that Temperature features have really high score of VIF. We first eliminate the feature with high score and re run VIF function to see if there is any change in the scores and repeat this process until all of the variables have a score <5
#If we write a function then we do not need to re run same set of lines all the time.After checking VIF scores we give the column name with high VIF score as an argument in this function and it is dropped form the dataframedef check_vif_drop_column(X,column_name):
X = X.drop(columns=column_name)
vif = pd.DataFrame()
vif[‘Features’] = X.columns
vif[‘VIF Factor’] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
return vif,Xvif1,X = check_vif_drop_column(X,’Temperature_Median’)
vif1

The VIF scores of Temperature_Min and Temperature_Max have decreased and lets eliminate Temperature_Min in this step as VIF is higher than Temperature_Max and recheck the scores
vif2,X = check_vif_drop_column(X,’Temperature_Min’)
vif2
Now all the variables have VIF scores allowed range, we can move to model building
We split the data into X_train,X_test,Y_train,Y_test.
- X_train,Y_train are used in training process and X_test,Y_test for testing the model.
- train_test_split function is imported from sklearn.model_selection which does the splitting job
- This function has a parameter ‘test_size’ that allows the user to set the proportion of data to be used for testing the model (here we use 0.25)
def split_train_data(X,Y):
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25)
return(X_train, X_test, Y_train, Y_test)X_train, X_test, Y_train, Y_test = split_train_data(X,Y)
As we have defined the data sets used for training and testing, we now move to model building. In sklearn we have all kinds of models as functions which we import and fit the data to train. We have already imported the LinearRegression() from sklearn.linear_model.
#Arguments will be the model used for training and train data.We can change this function according to the problem statement and requirement( remember to change it in argument too :P)def model_fit(model,X_train, Y_train):
model = LinearRegression()
model.fit(X_train, Y_train)
return modellin_model = model_fit(LinearRegression,X_train, Y_train)
The model has been trained and we need to predict with test data and validate it using different metrics
- model_name.predict(X) is used to predict the response variable.
- mean_squared_error and r2_score are calculated as discussed in section 1.3 in sklearn.metrics
- We check the scores for both X_train and X_test which means how good the model has predicted for train dataset and test data
def scores_(model,X,Y):
y_predict = model.predict(X)
rmse = (np.sqrt(mean_squared_error(Y, y_predict)))
r2 = r2_score(Y, y_predict)
print(‘RMSE is {}’.format(rmse))
print(‘R2 score is {}’.format(r2))print("The model performance of training set")
scores_(lin_model,X_train,Y_train)
print("--------------------------------------")
print("The model performance of testing set")
scores_(lin_model,X_test,Y_test)

3. Final Code
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_scorebeer_data=pd.read_csv(“beer_consumption_data.csv”)beer_data.columns=[“Date”,”Temperature_Median”,”Temperature_Min”,”Temperature_Max”,”Rainfall”,”Weekend”,”Consumption_litres”]beer_data[‘Temperature_Median’] = beer_data[‘Temperature_Median’].str.replace(‘,’, ‘.’).astype(‘float’)
beer_data[‘Temperature_Min’] = beer_data[‘Temperature_Min’].str.replace(‘,’, ‘.’).astype(‘float’)
beer_data[‘Temperature_Max’] = beer_data[‘Temperature_Max’].str.replace(‘,’, ‘.’).astype(‘float’)
beer_data[‘Rainfall’] = beer_data[‘Rainfall’].str.replace(‘,’, ‘.’).astype(‘float’)beer_data = data.dropna()X = beer_data.drop(columns=[‘Date’, ‘Consumption_litres’])
Y = beer_data[‘Consumption_litres’]plt.figure(figsize=(7,7))
sns.heatmap(X.corr())
plt.title(“Correlation Heatmap”)
plt.show()vif = pd.DataFrame() #Let us show th VIF scores in a data frame
vif[‘Features’] = X.columns
vif[‘VIF Factor’] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif)def check_vif_drop_column(X,column_name):
X = X.drop(columns=column_name)
vif = pd.DataFrame()
vif[‘Features’] = X.columns
vif[‘VIF Factor’] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
return vif,Xvif1,X = check_vif_drop_column(X,’Temperature_Median’)
print(vif1)vif2,X = check_vif_drop_column(X,’Temperature_Median’)
print(vif2)#Modellingdef split_train_data(X,Y):
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25)
return(X_train, X_test, Y_train, Y_test)def model_fit(LinearRegression,X_train, Y_train):
lin_model = LinearRegression()
lin_model.fit(X_train, Y_train)
return lin_modeldef scores_(lin_model,X,Y):
y_predict = lin_model.predict(X)
rmse = (np.sqrt(mean_squared_error(Y, y_predict)))
r2 = r2_score(Y, y_predict)
print(‘RMSE is {}’.format(rmse))
print(‘R2 score is {}’.format(r2))
X_train, X_test, Y_train, Y_test = split_train_data(X,Y)
lin_model = model_fit(LinearRegression,X_train, Y_train)print(“The model performance of training set”)
scores_(lin_model,X_train,Y_train)
print(“ — — — — — — — — — — — — — — — — — — — “)
print(“The model performance of testing set”)
scores_(lin_model,X_test,Y_test)
This data set fits properly with linear regression, but we find data sets which fits with high accuracy on train data set but when predicted with test data the accuracy is really low. This scenario is called overfitting and we will deal with it in this next blog
References: An Introduction to Statistical Learning: With Applications in R
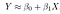
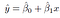
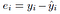
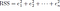


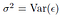



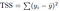
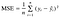








Comments
Post a Comment